简介
空间塔是用来存储一定范围内方块和实体的设备。(实质是将方块和实体搬入封闭空间)
这样可以在需要的时候调用出实体/方块来,或者搬运一些镐挖不掉的方块,如末地传送门框架。
1.16.x无法使用
在1.16.x版本中空间塔会无法使用,空间元件显示未格式化。
AE2只在高版本修复了这个Bug,你可以添加“附属”模组来解决这个问题:
https://www.curseforge.com/minecraft/mc-mods/dimension-update-fixer
能搬运的方块
默认情况下,含有NBT的方块无法搬运,无则可以。
AE2添加的黑白名单:
| 不能搬运的不含NBT方块 | 基岩。 |
| 能搬运的含NBT方块 | AE2的所有该类型方块、屏障、信标、酿造台、箱子、命令方块、比较器、阳光探测器、发射器、投掷器、附魔台、末影箱、熔炉、漏斗、刷怪笼、活塞、潜影箱、告示牌、头颅。 |
与AE2联动的模组通常会自行为黑白名单添加对应模组内容。
附属模组SpatialCompat则尝试使得所有方块都可以被搬运。
该结构需要的方块主要是 空间塔 方块(与结构同名)和 空间IO端口 。
搭建
空间柱、合格判定和SCS范围
空间柱有相关辞条,请查阅。
先观看一下合格的空间塔样例

越发扯淡
接下来是详细规则归纳总结。
(解释:下文中“内”指不在表面,如3*5*7的长方体“内”为1*3*5的空间)
找到网络中所有的空间柱,取构成空间柱的空间塔方块的最 上下东西南北 的坐标,构成长方体:

这个长方体内如果有该网络的空间柱 则不合格:
然后构成的长方体内则是SCS范围。如果内部空间不存在则不合格,如0x?x?。
补充:
SCS范围是记录坐标不记录维度!
空间柱的连接甚至可以跨量子环和P2P
(至于跨维度:方块的坐标正常记录,如主世界有一条空间柱,地狱也有一条,相当于主世界/地狱同时各存在两条。空间IO端口在哪个维度启动就搬走哪个维度的方块,下文会详细解释)


使用
在空间塔所在网络连接一个空间IO端口,在其中放入合适的空间存储元件,给予空间IO端口一个红石脉冲,则该空间IO端口所在维度的SCS范围内方块与空间元件的内存发生交换:
若空间元件为新的则分配一个id,SCS范围内所有可搬运的方块、实体都移动至封闭空间对应位置,原地留下空气。
若已用过则将空间元件对应封闭空间的位置上的方块、实体与主世界的进行交换。如果有无法搬运的方块则该坐标上不进行交换。
合适——对于新元件,SCS范围任意方向上都必须小于其最大长度,如3x3x17的SCS范围不适用于163空间元件。对于使用过的元件则SCS范围必须与元件的存储信息大小上完全一致,甚至不能旋转。
空间IO端口gui,在左侧放入元件:

里面显示了网络的总能量和最大能量,以及此空间塔进行一次存储所需的能量以及效率,效率越高,耗能越少,达到100%时最少,具体计算见下。


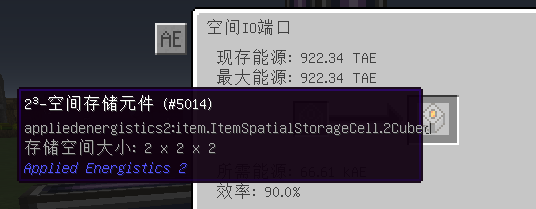
把这个元件取出再次放进空间IO端口,然后给予端口红石信号,则可释放出其储存的空间,并将现有的空间同时写入元件。
由此可以实现两个区域的相互转换,例如上面已经存入蓝色玻璃之后,在原有的区域放置橙色玻璃:

将存有蓝色玻璃的存储元件再次放进端口,按下按钮(给予红石信号),则橙色玻璃被蓝色玻璃替换:

这之后再次进行之前的操作则蓝色玻璃又会换成橙色玻璃,由此实现了两个空间的相互转换。
可以设置多个空间塔网络,配合物流系以及区块加载器进入封闭空间实现“传送器”的功能:

*在一个空旷的维度放置好空间柱,再在要进行空置/填充的维度放置ME空间IO端口,使用量子环连接,激活空间塔,便可以在ME空间IO端口所在维度进行大规模的方块操作,如空置地狱、填充末地等。
增加效率方案举例
(图中其实12棱就100%了)

频道、耗能
持续耗能:一个空间塔方块稳定耗能0.5AE/t;每个空间IO端口耗能1AE/t
单次激活能耗 (单位: AE) = minPower * efficiency ^ 0.25 + maxPower * ( 1 - efficiency ^ 0.25)
"^"为乘方运算。
单次激活空间塔要求网络中直接缓存有足够的AE能量,这通常意味着需搭配大量能源元件。
对于SCS范围为 x * y * z 的一个空间塔,vTower 为 (x+1)(y+1)(z+1)
基础能耗:minPower=vTower * spatialPowerMultiplier
附加能耗:maxPower = minPower ^ spatialPowerExponent
spatialPowerMultiplier 默认值为 1250,spatialPowerExponent 默认值为 1.35,二者都可通过配置文件中的同名参数项更改
效率:efficiency= 构成该空间塔的空间塔方块数量 / Max ( 6 , [ 3/8 * ((x+1)(y+1)+(x+1)(z+1)+(y+1)(z+1)) ] )
Max(a,b)表示取a、b两者中较大的,如Max(2,3)=3。
[ 3/8 * ((x+1)(y+1)+(x+1)(z+1)+(y+1)(z+1)) ] 一式向下取整,即仅保留整数部分。
综合上式,
当效率efficiency达到100%,单次激活仅消耗基础能耗minPower,
而当效率efficiency不足100%,对于一定的SCS范围,效率efficiency与构成该空间塔的空间塔方块数量成正比,单次激活总能耗随效率增长呈对数型下降。
对于较大的SCS范围,效率在90%~100%区间内时能耗仍能出现数量级上的差距,因此在仅考虑降低能耗时,应直接将效率推至100%。
而需要减少耗材时,考虑到能源元件与空间塔方块本身的耗材,通常在效率50~60%时,两者就会达到一定的平衡。
如下图,以一个128*128*128的SCS范围为例,可求得效率-单次激活能耗的曲线,在最低效率(只有6个空间塔方块)的情况下,需310942个致密能源元件;而当效率达到100%,则只要164个致密能源元件,但需要18432个空间塔元件。此时计算50%效率下的配置,可知需18432个能源元件以及14746个空间塔方块,耗材相对平衡。而对于能量,取10倍minPower时,所需求的的效率仍高达99.95%,100倍时效率需求才降至82%左右,可见需要节能时效率应尽量逼近100%。




